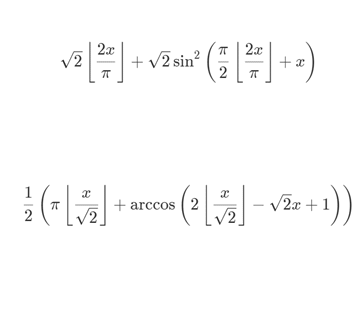【微分几何】正方形的弧长函数及其反函数

1、先来构造弧长函数：Floor[(2 x)/Pi] Sqrt[2] +Sqrt[2] Sin[x + Floor[(2 x)/Pi]*(Pi/2)]^2

3、试图通过解方程的方法，来求取反函数，结果是不能求取。

5、把这个求解结果，转化为分段函数，并绘制图像：ll[t_觥终柯计] :=Piecewise[{{1/2 ArcCos[(Sqrt[2] - 2 t)/Sqrt[2]], 0 <= t < Sqrt[2]}, {1/2 (2 \[Pi] - ArcCos[-((3 Sqrt[2] - 2 t)/Sqrt[2])]), Sqrt[2] <= t < 2 Sqrt[2]}, {1/2 (2 \[Pi] + ArcCos[(5 Sqrt[2] - 2 t)/Sqrt[2]]), 2 Sqrt[2] <= t < 3 Sqrt[2]}, {1/2 (4 \[Pi] - ArcCos[-((7 Sqrt[2] - 2 t)/Sqrt[2])]), 3 Sqrt[2] <= t < 4 Sqrt[2]}}]Plot[{l[x], ll[x]}, {x, 0, 2 Pi}, AspectRatio -> Automatic,PlotRange -> {{0, 2 Pi}, {0, 2 Pi}}, ImageSize -> {360, 360}]

7、通过图像可以证明，这个函数确实是弧长函数的反函数。